A first-order Markov chain process is characterized by the Markov property, which states that the conditional probability distribution for the system at the next time period depends only on the current state of the system, and not on the state of the system at any previous time periods.
A finite-state discrete-time Markov chain is a stochastic process that consists of a finite number of states and transition probabilities among the different states. The process evolves through successive time periods known as steps.
Definition: Discrete-time Markov Chain
Let a stochastic process $S = \{X_0, X_1, \cdots, X_n\}$ be a sequence of discrete random variables. Then the sequence $S$ is a Markov Chain if it satisfies the Markov property:
$$\begin{align}
\mathcal{P}(X_{t+1} = j | X_t = i, X_{t-1}, \cdots, X_1, X_0) &= \mathcal{P}(X_{t+1} = j | X_t = i) \nonumber \\
&= \mathcal{P}(X_{t} = j | X_{t-1} = i) \nonumber \\
&= \mathcal{P}(X_{1} = j | X_{0} = i) \ ,
\end{align}$$
for all $t=0,1,\cdots, n$ and all possible states $i, j = 1, \cdots, m$.
Thus, such a Markov chain process is memoryless. Consequently, it can be used for describing systems that follow a chain of linked events, where what happens next depends only on the current state of the system.
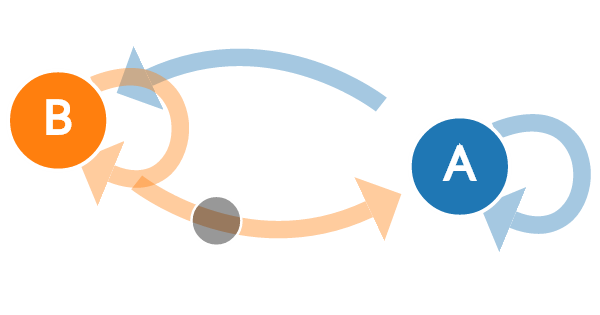 |
|---|
| A transition state diagram |
The Markov property is a sufficient condition for a stochastic process to be a Markov chain. However, it is not a necessary condition. For example, the random walk is a Markov chain, but it does not satisfy the Markov property.
A Markov chain with memory is a process satisfying,
\[\begin{align} \mathcal{P}(X_{t+1} = j | X_t = i, X_{t-1}, \cdots, X_1, X_0) = \mathcal{P}(X_{t+1} = j | X_t = i, X_{t-1}, \cdots, X_{n-p}) \nonumber \ , \end{align}\]for all $ n > p$. In this type of Markov chain, the future state depends on the past $p$ states where $p=1$ is equivalent to the usual Markov property.
A Markov chain is irreducible if there is a path from any state to any other state and aperiodic if the period of the chain is 1. A Markov chain is ergodic if it is both irreducible and aperiodic.
If the state space is finite, then the transition probability can be represented by a matrix $P$ whose $(i,j)$th element is given by:
\[\begin{align} P_{i j} = \mathcal{P}(X_{t+1} = j | X_t = i) \geq 0, \, \, \, \, \, \, \sum_{j=1}^m P_{i j} = 1 \ . \end{align}\]This matrix is also known as the one-step probability matrix, i.e. the $P_{i j}$ is the probability of moving from state $i$ to state $j$ in one-step in the chain. Similarly the $(i,j)$th element of the $k$-step probability matrix $P^{(k)}$ is,
\[\begin{align} P_{ij}^{(k)} &= \mathcal{P}(X_{t+k}=j | X_{t} = i) \ , \nonumber \\ &= \mathcal{P}(X_k = j | X_0 = i) \ , \nonumber \\ &\geq 0 \ , \end{align}\]and,
\[\begin{align} \sum_{j=1}^m P_{ij}^{(k)} = 1 \ , \, \, \, \text{ for }k = 0, \cdots, n \ . \end{align}\]This can be written in terms of the one-state transition matrix as $P_{ij}^{(k)} = (P^k)_{i j}$. As expected for $k=0,1$ we have,
\[\begin{align} P^{(0)} = I_m, \, \, \, \, P^{(1)} = P \ . \end{align}\]where $I_m$ is the $m \times m$ identity matrix and $P$ is the one-step transition matrix. The Chapman-Kolmogorov equation is,
\[\begin{align} P_{ij}^{(n)} = \sum_{\ell=1}^m P_{i \ell}^{(m)} P_{\ell j}^{(n-m)} \ . \end{align}\]This allows us to write the general property,
\[\begin{align} P^{(n + m)} = P^{(n)} P^{(m)} \ . \end{align}\]The steady state vector $\pi$ is defined as,
\[\begin{align} \lim_{n \rightarrow \infty} P_{ij}^{(n)} = \pi_j, \, \, \, \, \, \, \sum_{j=1}^m \pi_j = 1 \ . \end{align}\]We can determine this from the matrix equation,
\[\begin{align} \pi P = \pi \ . \end{align}\]The steady state vector is the eigenvector of $P$ with eigenvalue $1$. The steady state distribution is the probability distribution of the Markov chain at equilibrium and it is unique if the Markov chain is ergodic.
The expected number of steps to reach a given state $j$ from the initial state $i$ is given by,
\[\begin{align} \mathcal{E}(X_t = j | X_0 = i) = \sum_{k=0}^n k P_{ij}^{(k)} \ . \end{align}\]